The mean yearly rate is calculated by adding the monthly rate, and dividing the sum by the number of months. In Excel, it involves typing the equal sign in a cell, selecting the formula ‘AVERAGE’, and the range of cells.
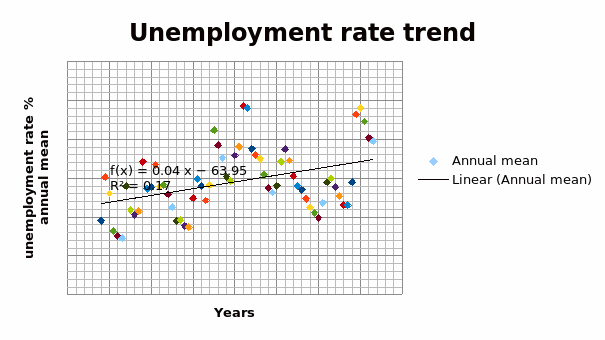
Regression analysis may be used to give estimates of values that are likely to occur in the future or to estimate missing values that occurred in the past. Keller (2012) explains that the line of best fit is derived from the least squares method. It is an approach that “minimizes the sum of the squared differences between points and the line” (Keller, 2012, p. 637). It creates a connection between a group of known values and the ones that are unknown.
Y-intercept
From observation, the y-intercept is approximately 4.7%. The y-intercept represents the point where the regression line cuts the vertical axis. From the graph, there are 2 units between 4% and 6%. There are also 5 small layers (boxes) vertically between 4 and 6. Each layer has a value of 0.4 (= 2 ÷ 5 layers). This shows that y-intercept which occurs 1 ¾ layers above 4 on the y-axis has a value of 4.7.
Slope
The slope can be calculated manually using the formula of slope which is the change in y/ change in x. The change in y can take any range but for this calculation it is the whole graph between 1948 and 2013. The change in y between this period is calculated by finding the difference between the values of y. These are 7.0 (for 2013) and 4.7 (for 1948). The change in y is 2.3 (= 7.0 – 4.7). The change in x is 65 (= 2013 – 1948). Applying the formula, the slope is 0.03538.
Alternatively, the slope can be calculated by typing the equal sign on a cell, selecting ‘SLOPE’ on the formula bar. Selecting the range of data, and clicking ‘OK’ on the slope formula box. The value it gives is 0.03524 which is almost similar to the one obtained from the manual calculations.
Equation of the linear regression line
In the simple regression technique, the estimate ŷ = bo + b1x. In this equation, ‘bo’ is the y-intercept, and ‘b1’ is the slope of the regression line. The equation of the regression line (ŷ = bo + b1x) becomes ŷ = 0.035x + 4.7.
2016 unemployment rate estimate
2016 is 68 years from 1948, ŷ = 0.035 (68) + 4.7 = 7.08. From this calculation, 2016 is expected to have an unemployment rate of about 7.08%.
Residual and standard error
The regression equation that incorporates the difference between the prediction and the actual value is y = β0 + β1x + e. The difference between actual value (yi) and estimate (ŷi) is known as the residual. The mean error is calculated by the formula which is the square root of Σ(yi- ŷi)2/(n-1), where yi is the yearly actual mean, and ŷi is the yearly estimate from the line of best fit (Keller, 2012).
‘1’ is subtracted from ‘n’ because of the assumption that the sample is drawn from the population. The population in this case would be all the years that unemployment has existed. In this case, y = 0.035x + 4.7 +/- 1.51.
My state is California which had an unemployment rate of 8.6% in May 2013 (Unemployment Rates, Seasonally Adjusted, 2013). It is an outlier. The data is credible because it almost matches the data presented on the government website for different states. For example, some states have high employment rates such as Illinois 9.1%. Others have low unemployment rates such as Hawaii 4.7%.
Others are within the range such Louisiana 6.8% (Unemployment Rates, Seasonally Adjusted, 2013). By incorporating the standard error, most values fall within the predictable range except those above 8.5% and those below 5.5% (= 6.98 +/- 1.51).
The data were extracted from the Bureau of Labor Statistics. They are derived from regular surveys conducted by the Bureau of Labor.
Interpretation of the analysis
A high unemployment rate reduces aggregate demand. The analysis shows that the retailer does not need to increase inventory by a large margin because increases in the unemployment level occurs at a very low rate.
Introduction to concept
The idea of managing inventory is to reduce costs associated with maintaining inventory, and to avoid interrupting service to customers because of a lack of products. Hmida, Regan & Lee (2013) explain that maintaining a high level of inventory that is not needed takes away resources from other uses that could have improved the company’s performance.
Keeping a low level of inventory also poses the threat of shortages which may result in loss of sales, and dissatisfied customers. In this situation, the retail company aims at predicting the unemployment rate to determine the level by which demand for its product may rise or fall. It is likely to fall because the unemployment rate is on an upward trend.
However, the unemployment rate has reduced between 2011 and the beginning of 2013. If it increases, the retailer needs to keep low levels of inventories. It should maintain the level extrapolated from the regression line because it captures the fluctuations experienced during the entire period. The regression analysis shows that the unemployment rate will increase by 0.04% from what it was in 2011 (from 6.94 to 6.98).
Keeping the right amount of inventory ensures a lower cost, and a smoothly running business. Chiang (2011) explains that unemployment may reduce demand. It may also reduce demand by a large margin of some type of products than others. The high unemployment rate implies less national income which creates less demand for money supply, and for products.
Inventories can also be managed by selecting commodities with the highest demand. The method is modified by combining it with other methods such as a mixed integer program (MIP) and multi-criteria classification to give a more reliable trend (Hmida, Regan & Lee, 2013).
Hmida, Regan & Lee (2013) discuss that the Just-in-Time (JIT) method may be applicable to some industries whose production is time related. JIT method involves receiving only the goods needed that meets the current demand. In the retail industry, the retailer has no control over production. The retailer needs to keep inventories that will prevent shortages.
When production is not based on time, JIT method may not be an accurate method of managing inventories because consumer demand may not be predictable, such as maintenance of ships. In this situation, predictability is set on the unemployment rate which affects consumer demand. JIT may be applied in this situation if producers maintain reliable levels of inventory or production is flexible which allows the retailer to receive goods within a short time after placing an order.
The retail industry may involve a maintenance program depending on the type of product or service. For example, a fast food industry may require some of its equipment repaired or replaced. Hmida, Regan & Lee (2013) explain that a preventive maintenance program should be used only if it costs less than the overall cost of repairing when an equipment has broken down. Retail industries may want to determine the best time to conduct a preventive maintenance process.
Adeyemi & Salami (2010) claim that when a retailer loses a customer today, future sales are also put at risk. Customer dissatisfaction may cause the customer to consider competitors’ products. In perishable goods retailing, excessive inventories may result in losses from spoilage or expiry of products (Adeyemi & Salami, 2010). Obsolescence may occur in the technology industry.
Goods may also be outdated in the fashion industry. The retailer may face the problem of clearing the stock. In such a case, discounts can be used to increase sales but it may result in losses (Deveshwar & Modi, n.d.). Keeping the right quantity for running businesses smoothly becomes necessary.
Gaur, Fisher & Raman (2005) discuss that products with a shorter life cycle tend to lack historical data. They also have a higher demand, and a higher price. They have a demand uncertainty, and require safety stock. Commodities with a long life cycle have a high inventory turnover than commodities with a shorter life cycle.
Keeping inventories also help to reduce ordering costs. In the Economic Order Quantity (EOQ) method, maintaining low levels of inventories may cause the retailer’s re-ordering frequency to be higher which increases ordering and carrying costs (Adeyemi & Salami 2010). These costs are included in the price of the product. When ordering costs are higher than inventory costs, it may be better to keep high inventories than minimizing ordering and carrying costs.
Some retailers already have space for keeping inventories. It would be cost efficient for them to keep a high level of inventories to reduce ordering and carrying costs. According to Adeyemi & Salami (2010) on their study of a bottling company, the usage of inventory increases as sales increase. Most manufactures have large warehouses making it flexible to use inventories according to their policies. Retailers may lack large spaces to manage inventory in a similar manner.
Deveshwar & Modi (n.d.) discusses that small businesses rely more on past experience and executive judgement to determine the amount of inventory to keep. Large companies use the EOQ model and linear programming to determine the level of inventories to keep.
Inventory management provides an effective and efficient method to plan the utilization of resources such as capital employees and equipment. Sales surprise is the unexpected rise in demand. Gaur, Fisher & Raman (2005) analyze that retailers expecting sales surprise tend to keep high inventories.
Factors that may change the regression line
One factor that may change the regression line is when the government gets involved in stimulus programs aimed at creating employment. Unemployment may decline, and national income may be higher to drive demand. Government can also reduce taxes which leave households with a higher disposable income. With a higher disposable income, households will have a higher purchasing power.
Another factor that can affect levels of unemployment is an innovation that increases efficiency in production or creates a new product. Examples of these are the discovery an efficient extraction method for shale gas, and technology products. Such discoveries may increase exports or reduce imports which may change the unemployment level.
Reference List
Adeyemi, S., & Salami, A. (2010). Inventory Management: A Tool for Optimizing Resources in a Manufacturing Industry, A Cases Study of Coca-Cola Bottling Company, Ilorin Plant. Journal of Social Sciences. 23(2), 135-142. Web.
Chiang, A. (2011). Multiple Unemployment Equilibria Under Non-representative Agent Demand. Stanford, CA: Stanford University.
Deveshwar, A., & Modi, D. (n.d.). Inventory Management: Delivering Profits through Stock Management. Web.
Gaur, V., Fisher, M., & Raman, A. (2005). An Econometric Analysis of Inventory Turnover Performance in Retail Services. Management Science. 51 (2), 181-194. Web.
Hmida, J., Regan, G., & Lee, J. (2013). Inventory Management and Maintenance in Offshore Vessel Industry. Journal of Industrial Engineering. 2013(10), 1-8. Web.
Keller, G. (2012). Statistics for Management and Economics. Mason, OH: South- Western Cengage Learning.
Unemployment Rates, Seasonally Adjusted. (2013). Web.