Empirical Analysis
Introduction
This analysis involves investigation the factors that affect the existence of gun related crimes. The data is collected for 49 states in the United States to help in this investigation. The data collected include the total number of fire arms in the US, the number of people living in poverty, number of people consuming alcohol, population between 18-24 years, and unemployment rate. The number of fire arms is the dependent variable while all the others are the independent variables. We seek to investigate if the independent variables have any significant effect on the dependent variable. The variables relate by the following model:
Crt = f (ACt, P1824t, PRt, UEt, )
The model can be expanded to give the following equation
Crt = β0 + β1ACt + β2P1824t + β3PRt + β4UEt + €t
This can also be represented by the following equation:
Y = β0 + β1X1 + β2X2 + β3X3 + β4X4 + β5X5 + €t
Where Y/ Crt is crime rate in year t, X1/ ACt
is alcohol consumption in year t, X2/ P1824t
is population between the age of 18 and 24 in the year t, X3/ PRt
is Poverty rate in the year t, X4/ UEt
is Unemployment rate for the year t, β5X5 is Brandy score/gun control and €t is the error term.
Regression Analysis
The analysis will be done using regressions analysis which will be done with the help of Eviews statistical software. The Eviews output were obtained as follows:
The estimated regression equation is represented as follows:
Y = -4.436524 + 2.38E-05 X1 – 9.18E-07 X2 + 0.000149 X3 + 0.092357 X4 + 0.158743 X5
S. E. = 13.14918 4.70E-05 3.54E-05 3.90E-05 0.169786 0.554915
t- Statistic =-0.337399 0.507321 -0.025964 3.810283 0.543962 0.286068
T-Test
To test whether each of the independent variables is an important determinant, we use t-test. The t-test for the sample of 49 elements will be done at n – k = 49 – 5 = 44 degrees of freedom. We test at 95% confidence level. The value of α = 5% which is the significance level. For this test, the critical value of t at df = 44 and α = 5% is 2.0154. The decision criterion for t-test is that if t- Statistic is greater than t-critical, we reject the null hypothesis. The hypothesis being tested is as follows
The null hypothesis is H0: β = 0, meaning that the independent variable is not an important determinant of the dependent variable
The alternative hypothesis is H1: β ≠ 0, meaning that the independent variable is an important determinant of the dependent variable.
We test every independent variable at a time
For X1, the t- Statistic < t-critical. In this case, we do not reject the null hypothesis. The conclusion is that X1 representing alcohol consumption is not an important determinant of Y (Crime rate).
For X2, t- Statistic < t-critical. We, therefore, do not reject the null hypothesis. This shows that X2 (population between the age of 18 and 24) is not an important determinant of Y (Crime rate).
For X3, t- Statistic > t-critical. The null hypothesis is thus rejected. We reject the alternative hypothesis and conclude that X3 (Poverty rate) is an important determinant of Y (Crime rate).
For X4, t- Statistic < t-critical. For this case, we do not reject the null hypothesis based on the decision criterion for t-test. We therefore reject the alternative hypothesis. This means that X4 (unemployment rate) is not an important determinant of Y (crime rate).
For X5, t- Statistic < t-critical. This means that we do not reject the null hypothesis. We conclude that X5 is not an important determinant of Y.
Interpretation of R squared and adjusted r squared
The value of R2, the coefficient of determination, is 93. 5355%. This means that the 93. 5355% of the variation in the dependent variable is explained jointly by the independent variables included in the regression. The R2 is said to have some problems that may lead to exaggerated results. The value of R2 increases with increase in the number of the independent variables even if they are not important. This means the results may be exaggerated and misleading. To solve this problem, adjusted R2 is used. In our case, R2 is 92.7838%. This means that 92.7838% of variation in Y is jointly explained by X1, X2, X3, X4, and X5.
F-test
This is a test of overall significance of the independent variables. The test aims at determining whether the variables are jointly insignificant. The null hypothesis tested he is as follows: H0: β0 = β1 = β2 = β3 = β4 = 0. The alternative hypothesis, therefore, will be
H1: β0 ≠ β1 ≠ β2 ≠ β3 ≠ β4 ≠ 0.
It is computed using the following formula:
F = (between – group variability) / (within – group variability )
In our case, F- statistic = 124.4334 which is the one computed as per the formula above. To validate the test, we obtain F- critical from the F- table at K-1 and N-K degrees of freedom. K is the number of samples in the system while N is the sample size. K-1 = 6 – 1 = 5. N – K = 49 – 6 = 43. The value of F in this case at α = 0.05 is 2.4322. The decision criterion is that if obtained F is greater than the critical F value, we reject the null hypothesis. In our case, F- statistic = 158.8357 and F- critical = 2.4322. Therefore, F- statistic > F- critical and we reject the null hypothesis. The conclusion in this case is that all independent variables jointly have a significant impact on the dependent variable. That is, β0 ≠ β1 ≠ β2 ≠ β3 ≠ β4 ≠ 0. The variables are not jointly insignificant.
Correlation matrix
Correlation is a statistical measure of relationships between two random variables. A correlation matrix is used to determine correlation coefficients where there are several variables in the model. For our case, the correlation matrix is stated as follows:
The correlation coefficients show that there are high degree relationships between variables. All independent variables are highly correlated with the independent variables. The correlation coefficients are over 0.9 meaning there is high correlation. This can be seen from the first column in correlation matrix above. The independent variables are also highly correlated with one another. For instance the correlation between X1 and X2 is 0.869810, X1 and X3 is 0.923163, X1 and X4 is 0.976301, X1 and X5 is 0.567789, X2 and X3 is 0.957522, X2 and X4 is 0.924903, X2 and X5 is 0.389256, X3 and X4 is 0.959688, X3 and X5 is 0.411871, and X4 and X5. Perfect correlation occurs when the correlation coefficient is equal to 1. This means that the independent variables are highly correlated because the correlation coefficients between them are close to 1, apart from those related to X5. This shows there is a problem of Multicollinearity that must be dealt with. This will be discussed in the next section.
Multicollinearity
This problem arises when there is a violation of the assumption of Ordinary Least Squares method of estimation. The assumption being violated is that there is no high correlation between independent variables that are used in the regression model. In our case above, we have seen that there is high correlation between the independent variables X2, X2, X3, X4, and X5. This means that Multicollinearity exists. In reality, this problem always exists but what matters most is the degree or magnitude. It should be minimized as much as possible. This problem arises because of improper use of dummy variable, using a variable in the model that is computed from other variables, including the same or almost the same variable twice, or just cases where variables are really and truly highly correlated. Our data suggests presence of Multicollinearity. Firstly, there are four independent variables but only one of the t-ratios of the coefficient is statistically significant. The irony is that the overall F-statistic is significant. Secondly, the t-ratios are too small and the value of R2 is high. There is also high correlation between the independent variables. To substantiate further the issue of Multicollinearity, we compute tolerance of the independent variables which helps us to calculate the Variance Inflation Factor, normally abbreviated as VIF. This concept is discussed in the section below.
VIF’s
The VIF shows the effect of Multicollinearity on the variance of the estimates in a model. It is computed by finding the reciprocal of the tolerance of the independent variables. Tolerance is compute as follows
Tolerance = 1- r2 Where r2 is the correlation between any two variables in the model. This is a good measure of Multicollinearity. A tolerance close to one means that multicollinearity is not a threat. If close to zero, multicollinearity is big. VIF = 1/Tolerance = 1/ (1- r2). There are computed in the table below:
From the correlation matrix below, we shall compute the tolerance and VIF.
From the above table, the values of tolerance are close to zero, meaning that there is high multicollinearity. We may also compute the VIF value for all the variables jointly as follows:
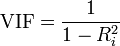
In this case, R2 is the coefficient of determination. Our R2 = 92.7838%. VIF = 1/ (1 – 0. 927838) = 13.858. The rule of thumb is that VIF > 5 means that multicollinearity exists and is of high degree. For the individual variables, it is clear that there is multicollinearity because all the values of VIF are greater than 5 apart from all correlations withX5.
Solution to multicollinearity
Existence of multicollinearity leaves the OLS estimates still unbiased and BLUE (Best Linear Unbiased Estimators). However, when it is high, the values of standard errors tend to be too small. This results to very small values of t-statistic. The danger in this case is that due to small t-ratios, the null hypothesis might never be rejected. It means the coefficients of the independent variables will have to be large enough for the null hypothesis to be rejected. There are a number of ways of solving multicollinearity but for this case we choose to remove some of the variables that are related. The variables that need to be removed are the one that is theoretically not sensible. Theoretically, the number of people living in poverty is believed to be a major determinant of crime rates. This has the same effect as the issue of unemployment in a country. When the level of unemployment is high, the number of crimes also increases. The gun control (X4) plays a role in reducing gun crimes. The population between 18-24 years does not necessarily mean that there are gun crimes. The same case with those consuming alcohol, they may not necessarily affect crime rates. We then remove two variables X2 and X1. We then have to run regression again and test the significance of the remaining variables. We, thus, regress Y against X3, X4, and X5. The Eviews output is as follows:
Y = β0 + β3X3 + β4X4 + β5X5
Y = -1.898519 + 0.000146X3 + 0.159076X4 + 0.225918 X4
S.E. = 12.07316 3.01E-05 0.099653 0.530858
T-Statistic =-0.157251 4.838890 1.596308 0.425572
The t-critical at 46 degrees of freedom and α = 0.05 is 2.0129. Based on this statistic, the t-statistic for X3 and X4 is greater than the critical value. We then reject the null hypothesis. Then we conclude that X3 and X4 are important determinants of Y. The t-statistic for X5 is less than t-critical. In this case, we do not reject the null hypothesis. Then we conclude that X5 is not an important determinant of Y. The F-test is done at α = 0.05 and 4-1 = 3 and 49 = 4 = 45 degrees of freedom. F-critical = 2.8115. F-statistic = 215.4167. F-statistic is greater than F-critical and thus we reject the null hypothesis. We conclude that X2, X3 and X4 are jointly important determinants of Y. The value of adjusted R2 is 93.0373 %, meaning that 93.0373% of variation in Y is jointly determined by X2, X3, and X4. We thus conclude that poverty and unemployment rates are significant determinants of crime rate. Brandy score is not a significant determinant of crime rate.