Determinant Factors for the Longevity of Humans Through Statistical Analysis Essay

Introduction

Simplify put, life expectancy has been said to be, ‘the number of years that an individual is expected to live as determined by statistics’ (Wilkinson, 1996, p.171; Banca, 2003, p.23). The years an individual could live are determined by actuaries. The calculations involving life expectancy are conducted during child births or other preferred times as desired. on a general note, it is expected that at birth, humans have the tendency to live up to eighty years, when as an individual who is 40 years could possibly live up to eighty-five years of age. The benefits accrued to projecting the expectations for how long individuals could live include the determination of the period s expected of individuals to attain retirement form work, and how long they continue to benefit from emoluments. Based on this notion, Belsley noted that:

‘Annuities payable for lifetimes are usually based on separate male or female tables, except that a qualified plan or trust must use unisex tables’ (Belsley, 1991, p.82).

For countries, the wide recognition is that the expectations for longevity of an individual are primarily determined by individual’s financial state of been, as well as healthiness- but most determining among these are the negative aspects of poor-health and poverty, which are quite known to interrelate (UNDP, 2003). It is however noted a misperception of the two as said:

‘…based on the experience of the last few generations, the assumption that rising prosperity remains the main source of improved standards of health throughout society constitutes some form of misconception’ (UNDP, 2003, p.64).

The usual believe is good health will continually follow a comfortable standard of living. But against this believe, it is noted that:

‘The misconception is that the only remaining relationship between income and health is the residual relationship between absolute poverty and ill-health’ (WorldBank, 2003, p.229).

These counteracting misconceptions have necessitated the need for a study on the actual facts that determine the longevity of individuals in a clearly defined statistical, comparative and computational manner. This paper, therefore, is a direct response through statistical determination of human longevity as applied to by factors that affect how long humans live. information on (i) Life expectancy at birth (years), (ii) Literacy Rate (% of people ages 15 and above), (iii) Infrastructure (% of rural population with access to water) and (iv) Gross National Income per capita from a random selection of thirty countries was obtained and imputed into a new excel spreadsheet, as well further analysis was conducted using eViews.

Methodology

This analysis was conducted using eViews on the following parameter:

• A (30 X 1) matrix Y represented the data on Life Expectancy; and
• A (30 X 4) matrix X as follows:
  • The first (30 X 1) column contained only the number 1;
  • The second (30 X 1) column represented the data on Literacy Rate;
  • The third (30 X 1) column represented the data on Infrastructure; and
  • The fourth (30 X 1) column represented the data on Gross National Income per capita.

Solutions to Questions

Calculation of the matrix (X’X)^-1X’Y

Supposing Y’s value is taken FROM Y-mean, anD AN effort is made towards finding out the possibility OF Any similarity in X’s deviation from X-mean causes a form of linearity, no mater how awkward the relationship of the linearity may occur, the variance of X – X-mean may not certainly be explained by the variation in Y – Y-mean; as a matter of fact, there could be a reasonably huge inexplicable difference which could constitute a huge estimation error. If this is the situation, the totaled squared errors could possibly be huge as well. Conversely to actualize an appealing fit, however with the imputation of numeric values, the ratio is then denoted by Explainable-change in Y/Total change in Y. This ratio is captured by the term R² through the following:

1. The term in the numerator, being only a part of the one in denominator, is the smaller of the two, and so R² is never greater than 1;
2. When there is hardly any linear relationship between X and Y, R² is low (close to 0) – on the other hand, a good linearity is an indicator of any change in the value of Y inferring that the numerator is nearer the denominator and R² is nearer to 1; and
3. R² = ( r_XY) ²

The following page contains a covariance/correlation/regression result from the age, GDP data (where R² is 0.3899, and suggests a poor fit):

Using EViews, the correlation coefficient r = 0.6244 between life expectancy and GDP is thus found:

It should be noted that r² = 0.389923 = R²

Regression

Hypothesis Testing

The BLUE property of the OLS estimates is used to test hypotheses about α and β; this involves testing the null hypothesis H_o: β = 0. Given a population regression equation;

Y = α + β X +Hε

The calculation of t-Statistic in this case is usually referred to as a t-ratio due to the fact that it is the ratio of the OLS estimator to its estimated standard error

In the present situation, β can not be zero; hence it could be either positive or negative because a priori, the direction of causality is not obvious

Therefore test is conducted of

H_o: β = 0 against H₁: β ≠ 0

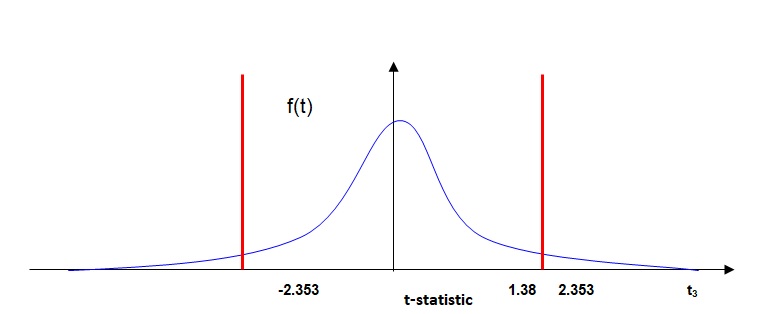
Because h₀ in the present case is sufficiently greater/smaller than zero, a two-tail test will be used (using a 0.05 level of significant, the critical t-value, with 3 d.o.f., is t_0.05 = 3.18). The decision criterion here is Reject H₀ if |t-Statistic| > 2.353

Given b = 19.46454 and s_b = 14.05681, t-Statistic = b/s_b = 19.46454/14.05681= 1.384707. The t-Statistic therefore is 1.384707, which is less than 2.353; hence reject H_o at the 0.05 level of significance is inappropriate (i.e. there is no evidence that Literacy Rate affects life expectancy. The following diagram implies:

Multivariate Regression Model

y = β_{0 n} + β1×1 + β2×2 + β3×3 +… + ε

y is the DEPENDENT variable where as each of the x_j is an INDEPENDENT variable- then, the following conditions are stated:

Each explanatory variable Xj is assumed:

(1A) to be deterministic or non-random; (1B): to come from a ‘fixed’ population; and (1C): to have a variance V(xj) which is not ‘too large’

Assumptions concerning the random term β_0, β_1, β_2, β_3.

(IIA) E(ε_i) = 0 for all I; (IIB) Var(ε_i) = σ² constant for all; IIC) Covariance (ε_i, ε_{k k}) = σ² for any i and k

(IID) each of ε_i has a normal distribution

Properties of b₀ , b₁ , b₂ , b_{3 :}

1. Each of these statistics is a linear function of the Y values;
2. Therefore, they all have normal distributions;
3. Each is an unbiased estimator [i.e, E(b_k) = b_0] b₁ and b₂
4. Each b_k is the most efficient estimator of all unbiased estimators

Thus, each of b₀ , b₁ , b₂ ….is:

Best; linear; unbiased; and estimator of the respective parameter

Conclusion

Each estimator b_i has a normal distribution with mean = β_{1 bi}² and variance = s_bi² where s_bi² is unknown

The Test (at 10% Significance) of the Hypothesis that ‘

Infrastructure has a positive effect on Life Expectancy at birth’

The proposed regression model is:

Life expectancy = ß₀ + ß₁(Literacy Rate) +ß₂(Infrastructure)+ ß₃(Gross National Income per capita)

It is hereby proposed that Life expectancy is the variable dependent on three independent variables:

Literacy Rate; Infrastructure; and Gross National Income per capita

The estimation of the proposed model is

Y^e = -1001.86 + 8.84* Infrastructure + 95.17* Literacy Rate + 1.51* Gross National Income per capita

Here Y^e is the estimated value of Life expectancy

The least-squares estimates of the ß-values are denoted by b-values; thus, b₁ is the estimate of ß₁ and b₂ is the estimate of ß₂ (in this present case, b₁ = 8.84, and b₂ = 95.17

Gross National Income Per Capita has an effect on Life Expectancy at Birth

Step 1: Set up of the hypotheses

H_0: ß₂ = 0 (Gross National Income per capita has no effect)

H_1: ß₂ > 0(Gross National Income per capita has a positive effect)

One-tailed test.

Step 2: Selection of statistic

The estimator b₂ is the test-statistic

Step3: Identification of the distribution of b₂

The above assumptions imply that b₂ is Best, and linear in the dependent variable income

Unbiased Estimator of b₂

Since b₂ is unbiased, E(b₂) = b₂

b₂ has a normal distribution because it is linear in Income

Thus, b₂~ N(b₂, b₂²) where b₂² is unknown.

Step 4: Construction of test statistic

_THE use OF the standard error of b₂ is employed here because the true value of b₂² is unknown

Therefore, the test statistic is t≡b (b₂– b₂) / (standard error of b₂) has a t-distribution with 20-4 = 16 d.o.f.

As b₂ = 0 under the null hypothesis (H0)t = b2 / (standard error of b₂)

Considering the regression output, it can be seen that b2 = 95.16913 and standard error of b2 = 38.53613. EViews therefore produces a t-statistic regarding Gross National Income per capit of 2.46907 (= 95.16914/38.53614.

The corresponding probability value is 0.0251.

Since this is a one-tail test, the half the probability value is accepted

^Step 5: Comparing with critical value t^C

t^C = 1.336756 for a one-tailed test with significance level = 0.1 and d.o.f. = 16

t^C = 1.336756 < 2.469606

Step 6: Conclusion drawn

The test is significant as follow: Rejection of H0 at 10% and at 5% (1.745883 < 2.469606) but not at 1% (2.583492 > 2.469607)

Step 7: Interpretation of result

It can be said that the data has been supported (with nearly 98% accuracy), hence the hypothesis that Gross National Income Per Capita has an effect on Life Expectancy at Birth is accepted.

Reference List

Banca, D., 2003. Survey on Italian Households Wealth and Income (SIHWI). Rome: Banca d’Italia.

Belsley, D., 1991. Conditioning diagnostics: collinearity and weak data in regression. New York: Wiley.

UNDP., 2003. Human Development Report 2003. New York: Oxford University Press.

Wilkinson, R., 1996. Unhealthy societies: the affliction of inequalities. London: Routledge.

WorldBank., 2003. World Development Indicators, 2003. Washington, DC: World Bank.