Abstract
This report presents the findings of a study commissioned by the dean of the College of Business at Bayview University. The objective of the study is to assess the current ethical behavior of business students at the university. The report concludes that cheating is a major problem among these students and that there is a need for a new study, which investigates why male students cheat more than their female counterparts do during their time at the university.
Introduction
Cheating at Bayview University and more specifically in the College of Business has been a pressing issue for the dean for quite some time. The concern is appreciable when consideration is made to a claim appearing in an article by the Chronicle of Higher Education that unethical behavior shown by Wall Street corporate officials, which can be attributed to prevalent cheating in business schools, played a role in the global recession of 2008 and 2009.
Faculty members have their opinions on the level of cheating in the university and the college. One group claims that in comparison to other universities cheating is more widespread in Bayview. Another group claims that the level of cheating in college is not a major problem. With these claims in mind, the dean commissioned a study targeting the students in the college. The main objective of the study is to assess the student’s current ethical behavior. Using statistical procedures and the data availed by an exit survey conducted as a part of the study this report discusses the nature of cheating at Bayview University’s College of Business.
Methods
Materials and participants
The study through an exit survey assesses three forms of cheating, which are captured in three of the four questions that make up the questionnaire of the exit survey. The valid responses to each of the three questions are “Yes” or “No”. It thus follows that if a student answers “Yes” to any of the questions then he or she is considered to have at one time engaged in some form(s) of cheating. The first of these three questions is “during your time at Bayview, did you ever present work copied off the Internet as your own?” (Anderson Winney & Williams, 2012, p. 397). The second of these three questions is “during your time in Bayview, did you ever copy answers off another student’s exam?” (Anderson et al, 2011, p. 397).
The third of these three questions is “during your time at Bayview, did you ever collaborate with other students on projects that were supposed to be completed individually?” (Anderson et al, 2011, p. 397). The fourth question in the survey is the gender of the respondent (student). The targeted and valid respondents are this year’s business graduating class students. From this population of respondents, a random sample of 90 students is taken who give their respective responses to each of the above questions.
Procedures
Statistical inference
Interval estimation
Interval estimation is one of the statistical inference techniques used in the preparation of this report. It is used to give the 95% confidence interval for three proportions that interest this report. The first is the proportion of all students involved in any of the forms of cheating assessed by the exit survey. The second proportion is that of male students involved in any of the forms of cheating assessed by the exit survey. The third proportion is that of female students involved in any of the forms of cheating assessed by the exit survey. According to Easton and McColl, “a confidence interval gives an estimated range of values, which is likely to include an unknown population parameter, the range being calculated from a given set of sample data” (n.d, para. 1).
According to Mason, Lind, and Marchal (1999), the confidence interval for a population proportion is estimated using the formula shown in appendix A (p. 287). In the formula, Mason et al (1999) specify that “p is the sample proportion, z is the z value of the degree of confidence selected and n is the sample size” (p. 287).
Statistical hypothesis testing
The other statistical inference technique that this report makes use of is statistical hypothesis testing. The definition of statistical hypothesis adopted by this report is given by Wyllys (2003), which is, “a statistical hypothesis is a statement about the value of a population parameter” (p. 1). Our parameter of interest is the population proportion which according to Mason et al (1999) gives the fraction of respondents who exhibit a particular behavior (p. 325). Two statistical hypotheses are stated and tested in this report.
The first hypothesis seeks to compare the level of cheating between business students of Bayview University and those of other institutions. According to Anderson et al (2012) “the Chronicle of Higher Education reported that 56% of business students in other institutions admitted to cheating at some time during their academic career” (p. 397). Letting P be the proportion of all business students of Bayview University who have cheated at one time during their stay at the university, this first hypothesis is stated as H0: P <0. 56 versus H1: P≥ 0.56.
The null hypothesis, H0, in this case, states that the level of cheating shown by business students at Bayview University is less than that of business students in other institutions. The alternative hypothesis, H1, in this case, states that the level of cheating shown by business students at Bayview University is equal to or greater than that of business students in other institutions.
The second hypothesis seeks to compare the level of cheating between business students of Bayview University and non-business students in other institutions. According to Anderson et al (2012) “the Chronicle of Higher Education reported that 47% of non-business students in other institutions admitted to cheating at some time during their academic career” (p. 397). Again, letting P be the population proportion of business students of Bayview University who have cheated at any time during their stay at the university, this second hypothesis is written as H0: P < 0.47 versus H1: P ≥ 0.47.
The null hypothesis, H0, in this case, states that the level of cheating shown by business students at Bayview University is below that of non-business students in other institutions. The alternative hypothesis, H1, states that the level of cheating shown by business students at Bayview University is equal to or greater than that of non-business students in other institutions. Four assumptions underlie the statistical hypotheses above (Mason et al, 1999, p. 325). The first assumption is that random variables obtained from the data are the result of counting the number of successes (the responses that interest us).
The second assumption is that each outcome of the survey falls into one of two mutually exclusive classes; “Yes” or “No” or “Male” or “Female”. The third assumption is that there is an equal chance of success in each interview process. The fourth assumption is that the interviews are independent, which means that the outcome of one interview does not affect the outcome of another. Mason et al (1999) further state that, for the above tests to be appropriate nP and n(1-P) should be greater or equal to 5; n being the sample size and P being the population proportion (p. 325). In the first hypothesis P = 0.56 and n = 90. In this case nP = 90(0.56) = 50.4 > 5 and n(1-P) = 90(1-0.56) = 39.6 > 5. In the second hypothesis P = 0.47 and n = 90. In this case nP = 90(0.47) = 42.3 > 5 and n(1-P) = 90(1-0.47) = 47.7 > 5. In both these hypotheses, nP and n(1-P) are greater than 5 making the tests appropriate.
The hypotheses above are being tested at a confidence level of 95% which implies a significance level of α = 0.05. The test statistic, z, for these hypotheses as given by Mason et al (1999) is shown in appendix B (p. 326). In the formula, Mason et al (1999) specify that “P is population proportion, p is the sample proportion and n is the sample size” (p. 326). The tests of these hypotheses are one-tailed and therefore H0 is rejected when z > zα. α = 0.05, zα = z0.05 = 1.65 hence H0 is rejected when z > 1.65. zα is gotten from the normal distribution table.
Microsoft Excel computations
The data from the exit survey is compiled into a Microsoft Excel dataset. The dataset has five columns. The first column, headed “Student”, holds the number of the student. The second column, headed “Copied from the Internet” holds the various responses given by each of the 90 students to the first question. The third column, headed “Copied on Exam” holds the various responses given by each of the 90 students to the second question. The fourth column, headed “Collaborated on Individual Project” holds the various responses given by each of the 90 students to the third question. The fifth column headed “Gender”, holds the gender of each of the 90 students interviewed. To compute the required sample proportions Excel’s COUNTIF and COUNTIFS functions are used on the data. The COUNTIF function gives a count of the number of cells in a specified range that meet a given criterion and the COUNTIFS function gives a count of the cells in a specified range that satisfy some criteria. The table in appendix C shows the use of these functions in the analysis of the exit survey data.
Results
Applying the above methodologies and using the COUNTIF and COUNTIFS functions as shown in the table in appendix C the following results are worked out. The results are given in a 2 decimal place format.
The sample proportion, p, of all students involved in some form of cheating is given by (16+18+29-6)/90 = 57/90 = 0.63. Using the formula given in appendix A, the fact that z = 1.65 and n = 90, the corresponding 95% confidence interval is = 0.63 ± 1.65√ ((0.63(1-0.63)/90) = (0.55, 0.71). The sample proportion, p, of male students involved in some form of cheating is given by (7+9+18-2)/90 = 32/90 = 0.36. Using the formula given in appendix A, the fact that z = 1.65 and n = 90, the corresponding 95% confidence interval is = 0.36 ± 1.65√ ((0.36(1-0.36)/90) = (0.28, 0.44). The sample proportion, p, of female students involved in some form of cheating is given by (9+9+11-4)/90 = 25/90 = 0.28. Using the formula given in appendix A, the fact that z = 1.65 and n = 90, the corresponding 95% confidence interval is = 0.28 ± 1.65√ ((0.28(1-0.28)/90) = (0.20, 0.36).
Using the formula shown in appendix B, the fact that p = 0.63, P = 0.56 and n = 90, the test statistic, z, for the first hypothesis H0: P <0. 56 versus H1: P≥ 0.56 becomes (0.63 – 0.56)/√ (0.63(1-0.63)/90) = 1.38. Since z < zα = 1.65 the null hypothesis, H0, is accepted. Using the formula shown in appendix B, the fact that p = 0.63, P = 0.47 and n = 90, the test statistic, z, for the second hypothesis H0: P <0. 47 versus H1: P≥ 0.47 becomes (0.63 – 0.47)/√ (0.63(1-0.63)/90) = 3.14. Since z > zα = 1.65 the null hypothesis, H0, is rejected.
Discussion
Accepting H0 in the first hypothesis means that the level of cheating shown by business students at Bayview University is less than that of business students in other institutions. Rejecting H0 and accepting H1 in the second hypothesis means that the level of cheating shown by business students at Bayview University is equal to or greater than that of non-business students in other institutions. The outcomes of these hypotheses tests imply that the percentage of cheating at Bayview University’s College of Business is ≥ 46% and < 57%. A comparison of the 95% confidence interval of male students involved in some form of cheating and that of female students reveals that male students cheat more than female students.
Conclusion
From the discussion above, it has been determined that the level of cheating in Bayview University’s College of Business is ≥ 46% and < 57%. This interval implies that half of the business students in the college engage in some form of cheating. Therefore, this report concludes that cheating is a major problem in Bayview University’s College of Business. With this conclusion made it is imperative that the college institute effective measures for discouraging cheating. If measures are in place their effectiveness should be one of the objectives of a subsequent study. It is also important for the college to emphasize to its students the need for ethics and ethical behavior.
The discussion section has also determined that male students cheat more than female students. Taking this into consideration this report concludes that there is a need for another study that seeks to investigate why this is so.
References
Anderson, D. R., Sweeney, D. J. & Williams, T. A. (2012). Statistics for business and economics. Ohio, USA: South-western Cengage Learning.
Easton, V. J. & McColl, J. H. (n.d). Statistics glossary: confidence intervals. Web.
Mason, R. D., Lind, D. A. & Marchall, W. G. (1999). Statistical techniques in business and economics (10 ed). USA: McGraw Hill.
Wyllys, R. E. (2003). Statistical hypothesis. Web.
Appendix
Appendix A
Appendix B
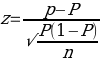
Appendix C
Table: Summary of the use of COUNTIF and COUNTIFS functions in analysis of survey data.