Background
This paper is a report on inferential statistics used to determine patterns inpatient discharges from U.S. public hospitals in 2019. The data were obtained from a primary source containing information on patient discharges by state (AHRQ, 2022). There are two sides to the paper’s statistical analysis at once: descriptive statistics are needed to examine general trends prevalent among the sample, while inferential statistics are used to examine statistically significant differences among subgroups.
Descriptive Statistics
Primarily, it is worth saying that the primary data for 2019 were represented by 36 rows, which for each state contained an individual number of patient discharges for that year. In other words, the data represented frequency variations in patient discharges by state within the United States. However, for some states, such as HI, ME, OR, and SC, no data were provided, and thus it was necessary to remove these lines from the statistical analysis. Thus, after the initial filtering procedure, the final number of lines in the sample was 32. Descriptive statistics showed that the mean number of patient discharges in 2019 for the states studied was 671,083, with a standard deviation of 784,700. A standard deviation more significant than the mean indicates an extremely high variance in the data in this set. In addition, the range was also used as a measure of variation. It was obtained that the distance between the maximum and minimum value of patient discharges in 2019 was 3,770,020. This means that for some states, such as California or Florida, the number of discharges is extremely high, while for other states, such as AK or VT, by contrast, the number of discharges is exceptionally low.
One-Way ANOVA
To use inferential statistics, the sample was divided into four subgroups, depending on the geographic location of the regions. Table 1 below shows summaries of measures of central tendency and variation for each of the subgroups used. At first glance, the average number of discharges is highest for Southern states and lowest for Northeastern, but this comparison is not sufficient to create definitive conclusions. For this reason, inferential statistics, namely a parametric ANOVA test, must be used. The choice of a one-way ANOVA test is due to the fact that the number of subgroups appears to be greater than two (LS, 2021). The null hypothesis postulates that all means are equal between each other, whereas the alternative hypothesis postulates that the means between groups are different. Table 2 shows the results of the ANOVA obtained using SPSS (Appendix B). The test result showed that there was insufficient evidence to convince us that there were statistically significant differences in the means between the groups. In other words, the mean values of all four subgroups showed no significant differences in patient discharges in 2019.
Table 1: Descriptive Statistics for the Four Subgroups
Table 2: Results of One-Way ANOVA for the Four Subgroups
An important assumption for the ANOVA test is the homogeneity of variance between groups. This assumption can be evaluated with the Levene test (LS, 2021). Appendix C shows the details of the test: Since the p-values were above the critical level of.05, the null hypothesis could not be rejected, and thus there were no differences in variance between the groups. In other words, the assumption of homogeneity of variances was met, so the test performed is reliable.
Paired T-Test
For the second step of the inferential statistics, a test was performed for differences in mean discharges between 2012 (M = 643,491, SD = 632,443) and 2019 (M = 671,083, SD = 784,700) patients. At first glance, there were differences between the averages as there were more discharges on average in 2019. Since only two groups were used this time, a paired t-test (KSU, 2021) was used. The results shown in Table 3 show that there was no difference in mean values between 2012 and 2019. In other words, in 2012 and 2019, the mean number of patient discharges was not statistically different.
Table 3: Paired T-Test results for 2019 and 2020
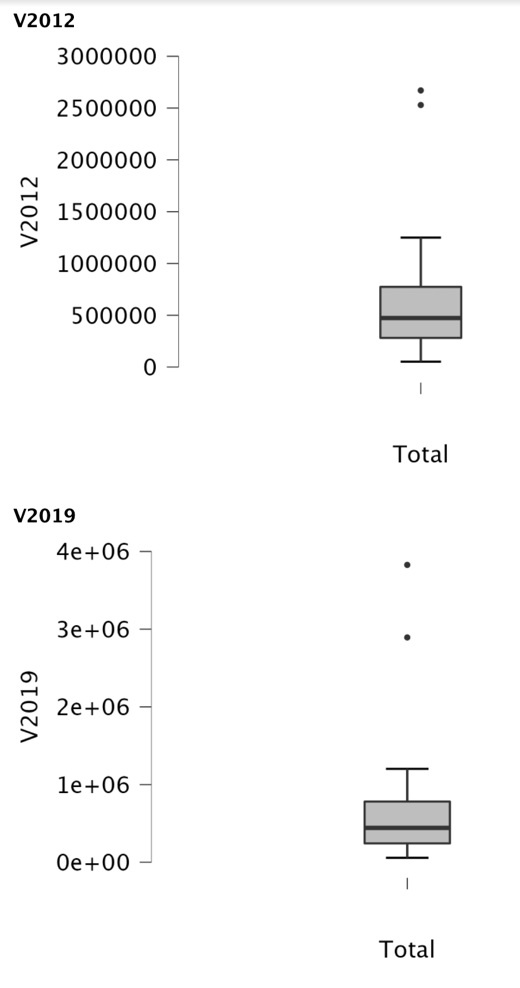
The main assumptions of the paired t-test are independence of observations, assumption of normality of distributions, and absence of extreme outliers. The latter can be checked by plotting boxplots — the presence of any outliers will be assessed visually (Zach, 2022). Figure 1 shows boxplots for two years: it is clearly visible that outliers were observed in both 2012 and 2019, which implies that the assumption of outliers was not satisfied.
References
AHRQ. (2022). HCUP state inpatient databases (SID) file composition — number of discharges by year. Agency for Healthcare Research and Quality. Web.
LS. (2021). One-way ANOVA in SPSS Statistics. Laerd Statistics. Web.
KSU. (2021). SPSS tutorials: Paired samples t-test. Kent State University. Web.
Zach, (2022). The three assumptions made in a paired t-test. Statology. Web.